kcorrect

From NYU CCPP Wiki

• 1 General description
• 2 What's new in v4
• 3 Conditions of use
• 4 Obtaining the software
• 5 Installing the software
• 6 Basic concept of obtaining K-corrections
• 7 IDL routines for SDSS, GALEX, 2MASS, DEEP2, and GOODS users
• 8 Lower-level IDL routines for K-corrections and photo-z's of arbitrary data
• 9 Other useful utilities in the IDL library
• 10 Stand-alone C code
• 11 kcorrect C library
• 12 Filter curves
• 13 Absolute calibration and its uncertainty in SDSS magnitudes
• 14 Linear relationships between different band systems
• 15 Known problems
• 16 Acknowledgements
• 17 Frequently Asked Questions

General description

This page describes the IDL version of the kcorrect software, which is no longer under development. There is now a Python version that you use instead.

The code and results are described in a paper in the Astronomical Journal.

This IDL code fits very restricted spectral energy distribution models to galaxy photometry or spectra in the restframe UV, optical and near-infrared. The main purpose of the fits are for calculating K-corrections, which the code does as well. The templates it uses for the fits may also be interpreted physically, since they are based on the Bruzual-Charlot stellar evolution synthesis codes. Thus, for each fit galaxy we can provide an estimate of the stellar mass-to-light ratio.

The easiest interface to the code, if it is available to you, is the IDL code. Detailed documentation is available for all of the routines. For users of the IDL version of the code, we have special high-level routines to handle data from a number of commonly used surveys: SDSS, GALEX, 2MASS, DEEP2 and GOODS. However, the lower level IDL routines are written generally enough that one can use those routine to handle data from any survey in the restframe UV, optical, or near-infrared.

The lowest level code compiles into a shared object library callable by C, so that non-IDL users can incorporate the K-correction routines directly into their code. It is possible in principle to link the C libraries into code based on SM, TCL/Tk, or Python, and I would be interested in helping interested parties to do this.

One can imagine using the results of this code to calculate the evolution of the luminosity function, the distribution of galaxy colors, as well as to develop galaxy classification algorithms.

What's new in v4

There are three main things that are new in the latest version:

1. The templates have been extended to work in the rest-frame ultraviolet, and still work in the optical and near infrared. In particular, our templates are consistent with data at low redshift from GALEX, SDSS, and 2MASS can be explained by our templates, and with data up to redshifts of 1.5 or 2.0 in DEEP2 and GOODS.
2. Because they are based on unaltered stellar evolution synthesis results from Bruzual-Charlot models, the fits have a natural physical meaning and one can make physical conclusions about recent star-formation histories and stellar masses.
3. The SDSS AB corrections have changed somewhat.
4. I have added a bunch of higher level IDL routines to perform common tasks, like K-correcting SDSS data, GOODS data, GALEX data, DEEP2 data, and 2MASS data, in addition to taking SDSS data and simulating DEEP2 or GOODS observations at higher redshift. When possible, users should stick to these high-level routines.

The new templates were obtained using a clever algorithm called "nonnegative matrix factorization," which finds the best set of N nonnegative templates which can be linearly, nonnegatively combined to explain a set of data. Think of it as "nonnegative PCA." However, it has the advantage over PCA that you can account explicitly for the uncertainties in the data. In our case, we use a basis set for the templates which consists of predictions of stellar evolution synthesis models, but you could simply use a set of discrete delta functions if you liked. This method has a bunch of potential applications in astronomy. The code is NMF_SPARSE in idlutils.

Conditions of use

Conditions of using the code released here are to send your email address to mb144@nyu.edu, to cite Blanton et al. 2007, and to specify the version tag (eg. v4_3) of the code used. (You can check this in the IDL code using the k_version command). Note that a previous version of the kcorrect paper existed (Blanton et al. 2003) which you need only cite if you are using v3_2 or earlier.

Obtaining the software

First off, if you are downloading the code, please register it. Do so by sending your email address to mb144@nyu.edu. No other information is required. I want this because it will allow me to contact users in case of any improvements or bug fixes.

Note that the IDL code depends on the idlutils package. The best way to obtain the code is to simply download the latest version from this site. The tagged and released versions, from latest to earliest, are:

• kcorrect.v4_3.tar.gz

Note that the repository for the code is managed on github.

Installing the software

The code has been tested, and compiles and runs on a Red Hat 7.1 OS. Little experimentation with other operating systems has been performed. Other Linux versions should port very easily, at least. In order to compile the code follow these directions:

First, set the environmental variables. For example, in bash:

KCORRECT_DIR=/usr/local/kcorrect
PATH=$KCORRECT_DIR/bin:$PATH
LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$KCORRECT_DIR/lib
export KCORRECT_DIR
export LD_LIBRARY_PATH
IDL_PATH=$IDL_PATH:+$KCORRECT_DIR/pro

or in tcsh:

setenv KCORRECT_DIR /usr/local/kcorrect
setenv PATH $KCORRECT_DIR/bin:$PATH
setenv LD_LIBRARY_PATH ${LD_LIBRARY_PATH}:$KCORRECT_DIR/lib
setenv IDL_PATH ${IDL_PATH}:+$KCORRECT_DIR/pro

These default settings may need to be changed on your system as follows:

1. KCORRECT_DIR: Simply substitute whatever directory you have downloaded this product into.
2. PATH: Obviously needed to run the binaries created
3. LD_LIBRARY_PATH: Required for the stand-alone code, so that the OS can find libkcorrect.so at runtime.
4. IDL_PATH: Set only if you are using IDL

You probably want to put these settings in your .bashrc or .tcshrc file. EvilUPS or UPS users can just type "setup -r /usr/local/kcorrect kcorrect"

Second, type "kevilmake -k" while in $KCORRECT_DIR. Then everything should compile At this point, you should be able to open IDL and start using the utilities described below, or run the stand-alone C code.

The IDL code depends on the idlutils package.

Note that the C codes "fit_coeffs.c" and "reconstruct_maggies.c" only depend on the K-correction library; thus, you can use them as templates for incorporating the K-correction code directly into your C code, as long as you include the K-correction library. In fact, you would probably put something like "fit_coeffs.c" into your code but include the k_reconstruct_maggies() call directly inside to get the K-corrections.

There is a known problem with compiling the stand-alone C code on a Mac OS X system. See Known problems for a description.

Basic concept of obtaining K-corrections

I'll describe the basic idea before getting into exactly how to use the code.

If you want to convert apparent magnitudes in band R to absolute magnitudes in band Q, you need to calculate the K-correction, which is defined by the equation:

m_R = M_Q + DM(z) + K_QR(z),

where m_R is the apparent magnitude, M_Q is the absolute magnitude, DM(z) is the distance modulus, accounting for the angular diameter distance and cosmological surface-brightness dimming, and K_QR(z) is the K-correction. By absolute magnitude we mean: the apparent magnitude in band Q the object would have if it were observed at rest, 10 pc away, using an aperture that contains its total flux. The distance modulus accounts for the difference between an object's actual distance and 10 pc. The K-correction accounts for the fact that you observed a redshifted galaxy in band R but the absolute magnitude requires a rest-frame observation in band Q. Obviously the difference between the fluxes observed in different bandpasses is fully determined by the galaxy SED and the description of the bandpasses. See Hogg et al. (2002) for a full description of what the K-correction is.

In order to get the appropriate SED for a set of galaxy fluxes, kcorrect fits an SED which is a nonnegative linear combination of some small number of templates. The templates have been optimized to minimize the residuals between the actual galaxy fluxes and the galaxy fluxes reconstructed from the galaxy SED fit. The units of the fit spectra created are in ergs cm⁻² s⁻¹ A⁻¹.

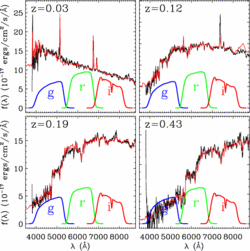
As an example, consider the figure below. I have taken actual spectra from the SDSS and projected them onto the g, r, and i bandpasses (since these are the ones the spectrum overlaps). Then I have run kcorrect (in this case version v3_2) and tried to reconstruct the spectrum. What kcorrect does here is to fit the nonnegative sum of three (carefully chosen) templates to the g, r, and i fluxes. The black line is the original spectrum, the red is the reconstructed. As you can see, the fit is reasonable.

I designed the code so it could calculate K-corrections from some set of observed AB bands to those same bands shifted by an arbitrary redshift, if so desired. For example, for the SDSS spectroscopic survey, most galaxies are observed near redshift 0.1; it makes sense, therefore, to K-correct to bandpasses shifted by 0.1 (ie. by a factor 1.1). This procedure minimizes errors in the estimated K-corrections, because the galaxies at z=0.1 will then have a K-correction which independent of their SEDs (and therefore their colors) and equal to −2.5log₁₀(1+0.1). In general, for a bandpass shifted by z_0, the K-correction for a galaxy at z_0 to the observed bandpass shifted by z_0 is −2.5log₁₀(1+z_0), independent of galaxy SED. A bandpass b shifted by redshift z is denoted ^zb (as in ^0.1g).

The inputs to the code are used AB maggies. These are the ratio of the source to the AB standard source in each band. To relate these quantities to magnitudes, an object with total flux f in maggies has magnitude

m = − 2.5 log ₁₀ f .

An advantage of the maggie unit system is that it is linear, and thus can when necessary accommodate negative flux estimates. Two notes:

1. As discussed below, SDSS catalog numbers are NOT on our best guess for the AB system. A set of offsets must be applied to the magnitudes to achieve our best guess. Our high level IDL code deals with this automatically.
2. SDSS catalog magnitudes obtained from the official survey database are luptitudes, which for reasonably bright objects are equivalent to magnitudes. While maggies are simply related to magnitudes by 10^−0.4m, the conversion from luptitudes to maggies is a bit more complicated; see the description accompanying the DR2 documentation). Our high level IDL code deals with these conversions automatically.

But you may still be wondering what I mean by an "AB" magnitude. The AB system is designed such that a flat spectrum object with f_ν = 3631 Jy = 3.631 × 10⁻²⁰ ergs cm⁻² s⁻¹ Hz⁻¹ should have every magnitude equal to zero. The beauty of the AB system is that the uniform definition makes it convenient to synthesize AB magnitudes from theory or models. The tragic flaw is that the quality of the AB-ness of a system is very dependent on precise spectrophotometry of standards and the carefulness of the calibrators, since no objects have a flat spectrum. There is a tension between these two needs --- similar to other tensions throughout astronomy between making precise measurements and making interpretable ones.

Finally, I have also included code to calculate photometric redshifts based on the templates. This procedure is as simple as running the K-correction code at each redshift and finding that redshift which provides the best fit in the χ² sense.

IDL routines for SDSS, GALEX, 2MASS, DEEP2, and GOODS users

The easiest interface to the code, if it is available to you, is the IDL code. The detailed documentation is available for all of the routines. The IDL code depends on the idlutils package.

The following routines exist:

1. sdss_kcorrect: SDSS K-corrections
2. sdss2bessell: Take SDSS ugriz fluxes and return Bessell UBVRI fluxes
3. sdss_kphotoz: SDSS photometric redshifts
4. galex_kcorrect: GALEX+SDSS K-corrections
5. twomass_kcorrect: 2MASS+SDSS K-corrections
6. gst_kcorrect: GALEX+SDSS+2MASS kcorrections
7. deep_kcorrect: DEEP K-corrections
8. sdss2deep: Take local SDSS observations and return fluxes which would be observed in DEEP at some given redshift.
9. goods_kcorrect: GOODS K-corrections
10. sdss2goods: Take local SDSS observations and return fluxes which would be observed in GOODS at some given redshift.

In all cases I have tried to make the inputs as close to the catalogs that the user might be using, and in the form of a structure passed by the user. The code calls routines like the following to handle the transformations:

1. sdss_to_maggies
2. galex_to_maggies
3. twomass_to_maggies
4. deep_to_maggies
5. goods_to_maggies

As noted in the documentation, these routines sometimes perform corrections to the AB system (such as the small corrections for the SDSS and the transformation from the Vega system in 2MASS). Also, they tend to add small uncertainties in quadrature with all of the uncertainties in order not to overfit to possible calibration errors. Sometimes they require the Schlegel, Finkbeiner and Davis dustmaps to be correctly installed on you system. Finally, they try to recognize the usual error flags and set inverse variances to zero where appropriate. The K-correction routines do output the maggies and inverse variances they calculate in the "omaggies" and "oivar" keywords.

In the case of SDSS, I provide both calibObj structure inputs (like those used by the Princeton reductions and the NYU-VAGC) and tsObj inputs (like those used by the Data Archive Servers). I don't ever use the Catalog Archive Server but would be happy to add an input structure for people who do if you let me know what columns to assume is in it. In the meanwhile, basically anything called "Counts" in the tsObj structure corresponds to anything called "Mag" in the CAS. Note the oddity that COUNTS_MODEL corresponds to modelMag.

These K-correction and photometric redshift routines will also return absolute magnitudes (and inverse variances of the same). To do so it assumes Ω_m = 0.3 and Ω_Λ = 0.7 (though these can be set differently on input). Absolute magnitudes are reported minus 5log₁₀(h) (where H_o = h*100 km/s/Mpc), with h=1 (ie, to use H₀=72 km/s/Mpc one has add 5log₁₀(.72) to the output of the code).

You will also note some outputs having to do with mass-to-light ratios and masses.

Lower-level IDL routines for K-corrections and photo-z's of arbitrary data

All the above K-correction and photometric redshift routines use the same basic engines, kcorrect and kphotoz. These routines uses SDSS filters by default but allow any type to be input. To perform K-corrections for other sets of bandpasses (say, the Bessell bandpasses or 2MASS bandpasses), look for them in $KCORRECT_DIR/data/filters and insert them in the filterlist= flag.

As an example of using kcorrect, one might do the following:

kcorrect, [1., 4.78, 10.96, 14.45, 19.05],  $
          [1100., 28., 7.7, 4.4, 2.5], $
          0.03, kcorrect, band_shift=0.1, chi2=chi2

which would take the set of maggies in the first argument, observed for a galaxy at redshift 0.03, and return the K-corrections to the ugriz magnitudes shifted by 0.1. This choice of maggies and uncertainties should return a good chi^2. Note that it is a nonnegative fit, so linear goodness of fit measures don't exactly apply.

Please note that kcorrect uses a lot of overhead (2-3 seconds worth), so if you can, use it on several thousand galaxies simultaneously at least. If you use it on each object individually (as in the example given above), you will be in trouble. If you truly cannot avoid it, then specify the extra arguments rmatrix and zvals. For example, if you run the following:

kcorrect, [1., 4.78, 10.96, 14.45, 19.05],  $
          [1100., 28., 7.7, 4.4, 2.5], $
          0.03, kcorrect, band_shift=0.1, chi2=chi2, $
          rmatrix=rmatrix, zvals=zvals, vname=vname
kcorrect, [1., 4.73, 11.26, 14.25, 18.85],  $
          [1100., 28., 7.7, 4.4, 2.5], $
          0.03, kcorrect, band_shift=0.1, chi2=chi2, $
          rmatrix=rmatrix, zvals=zvals, vname=vname

You will find that the second call takes far less time than the first, because the temporary data stored in rmatrix and zvals will not have to be regenerated. The high-level routines I discuss above all maintain common blocks which store rmatrix and zvals for you so you don't have to worry about this.

If you want to look at the fit spectrum, then specify vmatrix, lambda, and coeffs. The commands

kcorrect, [1., 4.78, 10.96, 14.45, 19.05],  $
          [1100., 28., 7.7, 4.4, 2.5], $
          0.03, kcorrect, band_shift=0.1, chi2=chi2, $
          vmatrix=vmatrix, lambda=lambda, coeffs=coeffs
plot, lambda, vmatrix#coeffs, xra=[2000., 12000.]

will plot the best fit spectrum. You can also just call k_load_vmatrix to get the templates.

If you want to project that spectrum onto a new set of bandpasses, use k_reconstruct_maggies. For example, to project back onto the SDSS bandpasses, the command

k_reconstruct_maggies, coeffs, 0.03, maggies, vmatrix=vmatrix, $
    lambda=lambda, filterlist=['sdss_u0.par', 'sdss_g0.par', $
    'sdss_r0.par', 'sdss_i0.par', 'sdss_z0.par']

will pass back the reconstruction in the array maggies. You can project onto any bandpasses you want. For example,

k_reconstruct_maggies, coeffs, 0.03, maggies, vmatrix=vmatrix, $
    lambda=lambda, filterlist=['bessell_B.par', 'bessell_V.par']
vega2ab=k_vega2ab(filterlist=['bessell_B.par', 'bessell_V.par'],/kurucz)
bessellmags=-2.5*alog10(maggies)-vega2ab
BminusV=bessellmags[0]-bessellmags[1]

will yield the Vega B-V for the best fit.

Fitting photometric redshifts just requires fitting the coefficients for a number of redshifts and minimizing the &chi² residuals for the fits. I provide the IDL routine kphotoz to do so (similar to the kcorrect routine). For example, one might do the following:

kphotoz, [1., 4.78, 10.96, 14.45, 19.05],  $
         [1100., 28., 7.7, 4.4, 2.5], $
         photoz

Again, there is large overhead, so one-at-a-time is not the way to call kphotoz. As for kcorrect, you can avoid spending this overhead more than once either by feeding it lists of objects or as follows:

kphotoz, [1., 4.78, 10.96, 14.45, 19.05],  $
         [1100., 28., 7.7, 4.4, 2.5], $
         photoz, rmatrix=rmatrix, zvals=zvals, vname=vname
kphotoz, [1., 4.78, 10.96, 14.45, 19.05],  $
         [1100., 28., 7.7, 4.4, 2.5], $
         photoz, rmatrix=rmatrix, zvals=zvals, vname=vname

By default, kphotoz uses a very simple prior (equal to the redshift z) to push the fits away from z=0. You can turn this off with the flag /noprior, or specify your own prior using the inputs zprior (which indicates the redshift grid) and lprior (which indicates the natural log of the prior).

A piece of advice on the type of magnitudes to use for SDSS photometric redshifts. For modern versions of PHOTO (v5_4 and later) it is best to simply use the model magnitudes for all galaxies. (And indeed this is what we use in sdss_kphotoz).

Users of kcorrect v3_2 will hopefully find that I retained backwards compatibility. Please note that the calling procedure has changed since v1_16, in the sense that inputting maggies is now the default.

Other useful utilities in the IDL library

In addition to the K-correction tools, kcorrect has some other useful tools in it:

1. k_project_filters() is a standalone IDL routine to project a spectrum onto a filter.
2. k_smooth smooths a spectrum with a Gaussian.
3. k_solar_magnitudes() calculates Solar absolute magnitudes in any filter.
4. k_vega2ab() provides conversions between AB and Vega magnitudes.
5. lf_distmod() calculates distance moduli given a redshift and cosmology.
6. A number of useful routines (mostly starting with "lf_") exist for calculating luminosity functions.
7. There are various pieces of code (not all written by me) for reading in certain types of data files, like Bruzual-Charlot predictions (by John Moustakas), Bruce Draine's PAH spectra, PEGASE2 predictions (by Alex Quintero), Witt-Gordon multiple-scattering dust extinction predictions, and Mappings-III style emission line fluxes.

Stand-alone C code

The C code requires a bit more attention to use. If people say they would use it if it were easier, I will improve it. In this section, I will describe the stand-alone C programs which fit for the coefficients and which calculate the reconstructed maggies. In the next section, I will briefly describe how to use the libraries within your own C code.

There are two stand-alone programs, fit_coeffs and reconstruct_maggies. fit_coeffs uses the maggies in each band to calculate the coefficients. reconstruct_maggies uses the list of coefficients (as output by fit_coeffs to reconstruct the magnitudes.

fit_coeffs has a help flag:

apeiron.[kcorrect].7 % fit_coeffs --help
Usage: cat  | fit_coeffs [--vfile vfile --lfile lfile
            --ffile ffile ]

As indicated, you would call it like

cat maggies.dat | fit_coeffs

where each line of "maggies.dat" has the form:

redshift umaggies gmaggies rmaggies imaggies zmaggies uinvvar ginvvar rinvvar iinvvar zinvvar

All of the quantities in this file are in maggies, as described above. So you have to convert the luptitudes or magnitudes --- and the inverse variances --- into maggies before calling this. (Note that the conversion to the inverse variances from the maggies and the magnitude errors is (0.4 ln(10) × maggies × magerr)^-2).

From the set of maggies and errors, the code calculates a set of four coefficients which correspond to its guess about the nature of the galaxy SED. The coefficients are output to standard out in the form:

redshift coeff0 coeff1 coeff2 coeff3 coeff4

where the redshift is included for reasons which will be clear soon.

Once you have the coefficients, you can calculate the reconstructed maggies for a galaxy with the same SED and same total flux, observed at any redshift through a shifted bandpass, using reconstruct_maggies. The help flag for reconstruct_maggies yields

apeiron.[kcorrect].8 % reconstruct_maggies --help
Usage: cat  | reconstruct_maggies [--vfile vfile --lfile lfile
            --ffile ffile --band-shift band_shift --redshift redshift]

So you can call it like:

cat coeffs.dat | reconstruct_maggies

where coeffs.dat is in the same format as the output to fit_coeffs:

redshift coeff0 coeff1 coeff2

The optional parameter "band_shift" specifies the bandpasses to reconstruct (band_shift=0., the default, indicates to use the observed frame bandpasses). "redshift" specifies the redshift at which to observe the galaxy (by default, the input redshift is used). The output is in the form:

redshift u_rec g_rec r_rec i_rec z_rec

in the original maggy units.

To summarize with an example, if you wanted to calculate the K-corrections from the observed bandpasses to rest-frame bandpasses shifted by 0.1, you could call the code as follows:

cat $KCORRECT_DIR/test/sample.dat | fit_coeffs | reconstruct_maggies >! maggies.dat
cat $KCORRECT_DIR/test/sample.dat | fit_coeffs | reconstruct_maggies --band-shift 0.1 --redshift 0. >! maggies.z0.dat

The K-corrections are then defined by −2.5 log₁₀(maggies/maggies.z0).

You can use the ffile option to reconstruct_maggies to specify a file which contains a list of the filters to use (by default, it uses the SDSS filters).

The stand-alone program fit_photoz works in the same way as fit_coeffs:

apeiron.[v3_1].27 % fit_photoz --help
Usage: cat  | fit_photoz [--vfile  --lfile
            --ffile  ]

As in:

cat maggies.dat | fit_photoz

where in this case each line of "maggies.dat" has the form:

umaggies gmaggies rmaggies imaggies zmaggies uinvvar ginvvar rinvvar iinvvar zinvvar

The output is again to standard out and is of the form:

photoz coeff0 coeff1 coeff2

The same rules apply here as to the IDL code: call the code for many objects at a time, or else the overhead (about 3 seconds) will kill you.

As I noted above, I have not worked very hard to make the stand-alone C code or the C library very usable, as generally speaking that would have meant replicating features in IDL and C, and I wasn't sure how many people would use the pure C versions. If there is a need to do this, I might be convinced to -- or if YOU do it, we could include your stuff in the library.

kcorrect C library

Why would you bother incorporating the K-correction code into your code at all, rather than just calculating the K-corrections once and reading in the results? Well, perhaps you have to calculate 1/Vmax, in which for each object you have to check its K-correction at (nearly) arbitrary redshifts. It is best to calculate the K-corrections on the fly in these cases, so we provide ways of doing this through a shared object libary.

For example, the stand-alone C code uses the "libkcorrect.so" library (in fact, this is *exactly* the same library which is linked into IDL). If you have this library in your LD_LIBRARY_PATH and you include the header file "kcorrect.h" (in $KCORRECT_DIR/include), your own code can call it. The best way to figure out how to use it is to read the examples in fit_coeffs.c and reconstruct_maggies.c, but I'll try to explain the essentials here.

1.First, the code has to have the basic information about the templates. You will usually be using the "default" templates in $KCORRECT_DIR/data/templates, so you will have to load in the files:

$KCORRECT_DIR/data/templates/vmatrix.default.dat
$KCORRECT_DIR/data/templates/lambda.default.dat

These files are in a special ASCII format which can be read into a "float*" variable in C using the routine k_load_ascii_table. For example:

k_load_ascii_table(&vmatrix,&ndim,&sizes,vmatrixfile);

loads in a set of data from vmatrixfile. The pointer to the data is returned in "vmatrix". The number of dimensions in the data is returned in "ndim". "sizes" is an array of size ndim giving the size of each dimension. The information in each of these files is the following:

• lambda.default.dat: The wavelength scale covered by the templates (the *edges*, not centers, of all pixels) [NLAMBDA+1]
• vmatrix.default.dat: The spectra spanning the SED space [NV,NLAMBDA]

2. Second, it is necessary to read in the filters. The list of filters is in the directory:

$KCORRECT_DIR/data/templates/sdss_filters.dat

This list is read by the routine "k_load_filters", which assumes all the filters are in the directory $KCORRECT_DIR/data/filters (or if KCORRECT_DIR is not set, in the current directory). This routine is called as:

k_load_filters(&filter_n,&filter_lambda,&filter_pass,&maxn,&nk,filterfile);

"nk" is the number of filters. "filter_n" is the number of points in each filter curve, "filter_lambda" is the wavelength scale of each filter, and "filter_pass" is the response curve of each filter. "maxn" is the maximum of "filter_n". This sets the indexing of "filter_lambda" and "filter_pass", so that to get the ith wavelength of the kth filter you access "filter_lambda[k*maxn+i]".

3. Third, you have to define the redshift range over which you are going to define a look-up table. I usually use 0. to 1., to be safe, with 1000 steps, using the code:

zvals=(float *) malloc(nz*sizeof(float));
for(i=0;i<nz;i++)
  zvals[i]=zmin+(zmax-zmin)*((float)i+0.5)/(float)nz;

where nz=1000, zmin=0., and zmax=1.

4. Finally, you have to define the look-up table which tabulates the projection of each basis element in the bmatrix onto each filter, at each redshift in zvals:

rmatrix=(float *) malloc(nz*nv*nk*sizeof(float));
k_projection_table(rmatrix,nk,nv,vmatrix,lambda,nl,zvals,nz,filter_n,
                   filter_lambda,filter_pass,band_shift,maxn);

One defines "nv" and "nl" based on the "sizes" returned by the k_load_ascii_table calls described above.

Once this overhead has been taken care of (and it is a significant amount of time --- a few seconds --- so only do it once!) you can use the routines k_fit_nonneg and k_reconstruct_maggies.

k_fit_nonneg is called as:

k_fit_nonneg(coeffs, rmatrix, nk, nv, zvals, nz, maggies, maggies_ivar,
            redshift, ngalaxy, tolerance, maxiter, niter, chi2,
            verbose)

The array coeffs should be of the size (nv*ngalaxy), and the coefficients are returned in it.

k_reconstruct_maggies is called as:

k_reconstruct_maggies(zvals, nz, rmatrix, nk, nv, coeffs, redshift,
                      reconstruct_maggies, ngalaxy)

where reconstruct_maggies are expressed in maggies.

The photo-z code can also be accessed through the C library libkcorrect.so. Instead of k_fit_coeffs, you will be calling k_fit_photoz, as in:

k_fit_photoz(photoz, coeffs, rmatrix, nk, nv, zprior, lprior, nprior,
             zvals, nz, maggies, maggies_ivar, ngalaxy, tolerance,
             maxiter, niter, chi2, verbose)

zprior, lprior, and nprior should contain the prior grid to use.

As I noted above, I have not worked very hard to make the stand-alone C code or the C library very usable, as generally speaking that would have meant replicating features in IDL and C, and I wasn't sure how many people would use the pure C versions. If there is a need to do this, I might be convinced to -- or if YOU do it, we could include your stuff in the library.

Filter curves

It is of course necessary to have filter responses to do any of this work. Thus, in kcorrect I have put together a fairly large library of filter curves in a homogeneous format. I have tried as far as possible to provide the provenance of all of these curves, though it has not always been possible to figure out.

The files are in a special SDSS format called FTCL described at the SDSS DR2 site. IDL code (in particular, yanny_readone()) exists in idlutils to read in such files.

It turns out that the SDSS filters do not have the responses they were designed to have, but Mamoru Doi has done the hard work of measuring them. Jim Gunn then took these, ran them through models of the telescope and the atmosphere (using an appropriately scaled model of the Palomar atmospheric model at airmass 1.3). Daniel Eisenstein deserves special mention for the extensive testing he has done on these. We have a repository of these and other curves. For kcorrect we use the SDSS files:

sdss_u0.par
sdss_g0.par
sdss_r0.par
sdss_i0.par
sdss_z0.par

The other SDSS files refer to the responses for each camcol.

Absolute calibration and its uncertainty in SDSS magnitudes

Our best estimate (from Eisenstein's work on hot white dwarfs) of the absolute calibration of SDSS data indicates that the magnitudes output by the SDSS pipeline code are not exactly on an AB system. There are offsets Delta m = m_AB - m_SDSS = [-0.036, 0.012, 0.010, 0.028, 0.040] in u, g, r, i, and z bands. Note these numbers have changed since v3_2. We have trained our templates on SDSS magnitudes corrected to this system. For the moment we recommend that the user apply these corrections to the magnitudes they are using.

In addition, we always apply minimum uncertainty of [0.05, 0.02, 0.02, 0.02, 0.03] mag in ugriz (the high level routines SDSS_KCORRECT, etc. already do so). This is because there is always an uncertainty in the calibration of any given galaxy, and we don't want the templates working super-hard to fit (say) some unrealistically small error bar in one band at the expense of the other bands.

Linear relationships between different band systems

Using this code on a number of SDSS galaxies, we have estimated the linear relationships between a number of different bandpass systems. The kcorrect paper has a table with these relationships.

Known problems

14. The sdss_kcorrect.pro utility documentation string claims that its "mag" and "err" inputs should be in asinh magnitudes. However, it treats them as Pogson magnitudes. To correctly use the "mag" and "err" inputs (as opposed to inputting fluxes or structures), those should be Pogson magnitudes. Thanks to Patricio Gallardo for pointing this out!

13. Russell Jurek reports the following, which I believe is applicable to Mac OS X 10.9 and kcorrect v4_2 or later. Thanks to Anne Jaskot for pointing this out.

 kcorrect: kcorrect installs using a `kevilmake' script in the installation's bin directory. 
 I had to tweak the kevilmake script in order to get it to compile. I changed the F77 
 compiler from g77 to gfortan, which negates the need to use the -lcc_dynamic compiler 
 flag. Delete all mention of -lcc_dynamic in the compiler flags, otherwise you'll get errors 
 and the library won't build. Don't forget to follow the instructions and comment in both 
 sets of lines required to compile the kcorrect C library. Note that I've only confirmed that 
 this will allow me to compile/create the kcorrect C library.

12. Edd Edmondson and Tom Melvin report that with v4_2 and IDL 8.1 on Ubuntu 10.04.4, there is a problem with building libkcorrect.so:

 undefined reference to `__stack_chk_fail_local'

They report that the code builds if X_CFLAGS for Linux in kevilmake includes:

 -fno-stack-protector

11. In v4_2 and earlier, the default compilation flags don't work for Mac OS X Lion (Darwin version == 11). Marla Geha tells us that adding the following works:

      if [ `uname -r | cut -c 1,2` == 11 ]; then
                LD=gcc
                X_LD_FLAGS="-dynamiclib -undefined dynamic_lookup -force_cpusubtype_ANY -single_module"
      fi

10. In v4_2 and earlier, the routine deep_kcorrect.pro does not treat the "filterlist" input correctly. Thanks to Joanna Woo for pointing this out. If it is once called with a given filterlist input during an IDL session, it will keep using that filterlist forever, no matter what inputs you give it. This will be fixed in future releases, but for now can be fixed by changing the common block:

 common com_deep_kcorrect, out_rmatrix, out_zvals, band_shift, $
   deep_rmatrix, deep_zvals, vname, out_filterlist

9. In v4_2 and earlier, the DEEP2 filters are incorrect (per energy instead of per photon). The versions on the kcorrect trunk are correct. (Thanks to Renbin Yan for fixing).

8. In v4_2 and earlier, kevilmake parses 'uname -r' incorrectly when building on Snow Leopard or above (any Darwin version >= 10). Users will want to edit kevilmake to force the 64-bit option. Genevieve Graves kindly solved this problem:

      "Darwin" )
              F77=g77
              SO_EXT=dylib
              X_LD_FLAGS="-bundle /usr/lib/bundle1.o -L/usr/lib  
-L/usr/lib/gcc/powerpc-apple-darwin8/4.0.0 -lc -lgcc -flat_namespace 
-undefined suppress"
              X_CFLAGS="-g -Wall -dynamic"
              if [ `uname -r | cut -c 1` \< 8 ]; then
                      X_LD_FLAGS="-bundle /usr/lib/bundle1.o -L/usr/lib 
-lc -lcc_dynamic -flat_namespace -undefined suppress"
#      Uncomment the following two lines to get .dylib libraries that 
can
#      be linked into C programs on a Mac OS X system
#                  LD=libtool
#                  X_LD_FLAGS="-dynamic -L/usr/lib -lc -lcc_dynamic"
              fi
              if [ `uname -r | cut -c 1` == 9 ]; then
                X_LD_FLAGS="-bundle -flat_namespace -undefined suppress"
#      Uncomment the following two lines to get .dylib libraries that 
can
#      be linked into C programs on a Mac OS X system
#     LD=libtool
#     X_LD_FLAGS="-dynamic -L/usr/lib -lc "
              fi
              if [ `uname -r | cut -c 1,2` == 10 ]; then
                  LD=libtool
                  X_LD_FLAGS="-dynamic -L/usr/lib -lc "
              fi
              SDSS_CFLAGS= ;;

7. In v4_2 and earlier, Linux 64-bit boxes fail with the message:

ld -shared -o /u/rreyes/IDL/kcorrect/lib/libkcorrect.so 
idl_k_projection_table.o k_projection_table.o idl_k_fit_spec.o 
k_fit_spec.o idl_k_fit_nonneg.o k_fit_nonneg.o idl_k_fit_photoz.o 
k_fit_photoz.o idl_k_reconstruct_maggies.o k_reconstruct_maggies.o 
k_strparse.o k_yanny_readone.o k_filter_struct.o k_fileopen.o 
k_load_filters.o k_read_ascii_table.o k_nonneg_solve.o k_interpolate.o 
idl_k_binspec.o k_binspec.o k_utils.o k_qromo.o k_midpnt.o k_choldc.o 
k_cholsl.o k_locate.o k_brent.o k_evolve.o k_zbrent.o k_polint.o 
idl_lf_calc_vmax.o idl_ztoV.o idl_Vtoz.o idl_z2dm.o idl_z2t.o idl_t2z.o 
idl_lf_eep.o idl_lf_select_eep.o ztransform.o iterate_lf.o philike.o 
phierrors_lf.o gaussj.o lf_select_eep.o lf_calc_vmax.o lf_eep.o 
lf_eepfit.o lf_WH_interp.o lf_set_AB.o lf_sum_AB.o
ld: k_projection_table.o: relocation R_X86_64_32 against `k_midpnt' can 
not be used when making a shared object; recompile with -fPIC
k_projection_table.o: could not read symbols: Bad value
make[1]: *** [/u/rreyes/IDL/kcorrect/lib/libkcorrect.so] Error 1

You want to edit the Linux section of kevilmake so it reads:

	"Linux" )
		SO_EXT=so
		X_CFLAGS="-fPIC -g -Wall"
		X_FFLAGS="-ffixed-line-length-none"
		SDSS_CFLAGS=
		X_LD_FLAGS=-shared ;;

Or just use the idlutils "evilmake" utility (if you are using the IDL version of kcorrect you need idlutils installed anyway).

6. There is a known problem with compiling the stand-alone C code on a Mac OS X 10.4 system or earlier, which results in the following error message:

cc -I/Users/blanton/kcorrect/include -I/Users/blanton/kcorrect/src -g
-Wall -dy namic -O3 -DCHECK_LEAKS -o
/Users/blanton/kcorrect/bin/fit_photoz fit_photoz.c - lm
-L/Users/blanton/kcorrect/lib \ -lkcorrect ld:
/Users/blanton/kcorrect/lib/libkcorrect.dylib is input for the dynamic
link editor, is not relocatable by the static link editor again make:
*** [/Users/blanton/kcorrect/bin/fit_photoz] Error 1 make: Target
`all' not remade because of errors. 

I am honestly not really sure what causes this. The library libkcorrect.dylib is fine for importing into IDL but NOT for importing into the stand-alone C code. If you want the library to be built correctly for importing into C programs, you can uncomment the two lines in the "kevilmake" script:

#   Uncomment the following two lines to get .dylib libraries that can
#   be linked into C programs on a Mac OS X system
#		LD=libtool
#		X_LD_FLAGS="-dynamic -L/usr/lib -lc -lcc_dynamic"

In this case, the library will be fine for importing into C but no good for using from IDL. I can't make the Mac do both with a single library file. Sorry! If somebody knows how to do this, PLEASE let me know.

4. In Mac OS X 10.5 (Leopard), there occurred some changes to the gcc libraries, which require the following addition to "kevilmake" at the end of the "Darwin" section:

    if [ `uname -r | cut -c 1` == 9 ]; then
     X_LD_FLAGS="-bundle -flat_namespace -undefined suppress"
#      Uncomment the following two lines to get .dylib libraries that can
#      be linked into C programs on a Mac OS X system
#     LD=libtool
#     X_LD_FLAGS="-dynamic -L/usr/lib -lc "
   fi

5. In v3_2 and earlier, fit_coeffs sends output to stdout occasionally of the form:

ERROR: choldc failed (sum==-1.197184e+06)

which screws up the inputs to reconstruct_maggies. If this affects you, change the line in k_choldc.c:

printf("ERROR: choldc failed (sum==%e)\n",sum);

to

fprintf(stderr, "ERROR: choldc failed (sum==%e)\n",sum);

4. In versions v1_10 and earlier, the code returned K-corrections to non-AB systems (oops!). Back in those days, Ivan Baldry pointed out that kcorrect returned non-AB magnitudes when it was requested to output K-corrections to shifted bandpasses. The sense of the error was that the K-correction was missing a term of −2.5 log₁₀ (1+z) for a bandpass shift of z_0. This error occurred independent of bandpass, color, redshift, and anything else. Thus, when interpreting magnitudes returned by kcorrect v1_10 and earlier, please apply a correction of −2.5 log₁₀ (1+z), where z_0 is the shift of the bandpass (eg. ^zb is the b-band shifted by z). Luckily this only is an error in the absolute measures of magnitude; colors are unchanged, the shapes of LFs are unchanged (just shifted in magnitude), etc. Many thanks to Ivan for pointing out the error.

3. In v4_1_4 and earlier, the twomass_*.par filter curves are off by a factor of lambda, because apparently the 2MASS web site posted energy-counting filter curves (but called them photon-counting). Fixed in v4_2 and later.

2. In v4_1_4 and earlier, there was a problem with calculating projections onto bandpasses that caused in some cases "jitter" (high frequency noise as a function of redshift at the sub-percent level). Fixed in v4_2 and later.

1. In v4_2 and earlier, a bug exists in sdss_kphotoz.pro, where "mags" on line 146 should read "mag." This affects the usage of magnitude inputs into the code instead of maggies. Thanks to Jon Loveday for pointing out the error.

Acknowledgements

This work was funded in part by a GALEX Archival research grant (Program 38).

Sam Roweis provided irreplaceable help in teaching me the algorithms used in this code. David Hogg tracked down many of the bandpass responses given here. Ivan Baldry was critical to debugging the code. Hewett and Warren provided a bandpass response for the b_j band. Thanks to Alison Coil, Jeff Newman, and Risa Wechsler for help understand and using the DEEP2 data. Thanks to Lexi Moustakas for help using the GOODS catalog -- and the GOODS team for access to that catalog. Thanks to John Moustakas for his code for reading in Bruzual-Charlot templates.

Funding for the Sloan Digital Sky Survey (SDSS) has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/.

The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, University of Pittsburgh, Princeton University, the United States Naval Observatory, and the University of Washington.

This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

The Galaxy Evolution Explorer (GALEX) is a NASA Small Explorer. The mission was developed in cooperation with the Centre National d'Etudes Spatiales of France and the Korean Ministry of Science and Technology.

DEEP2 is a collaboration between UC Santa Cruz and UC Berkeley. Funding for the DEEP2 survey has been provided by NSF grant AST-0071048 and AST-0071198. (Some of) the data presented herein were obtained at the W.M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W.M. Keck Foundation. The DEEP2 team and Keck Observatory acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community and appreciate the opportunity to conduct observations from this mountain.

Frequently Asked Questions

Why do I get a compilation error in K_LOAD_FILTERS?

filter_str=yanny_readone(curr_path+'/'+filterlist[i],hdr=hdr, $    
                                                              ^
% Syntax error.
 At: /Applications/kcorrect/pro/utils/k_load_filters.pro, Line 70 
% 1 Compilation error(s) in module K_LOAD_FILTERS.

Because you do not have idlutils installed. Install the idlutils package (you don't need the idlspec2d or anything else described on the above web page).

kcorrect assumes h=1. How do I change that?

For calculating absolute magnitudes, kcorrect uses a Hubble constant H₀ = 100h km/s/Mpc with h = 1, whereas in the actual Universe h = 0.7 or so. In order to convert the kcorrect outputs to your desired value of h you need to apply the term:

M(h) = M(h = 1) + 5log₁₀h

In this formula M(h = 1) is the output of kcorrect and M(h) is the absolute magnitude you want. That is, for a fixed flux the actual absolute magnitudes are brighter (i.e. you have to subtract about 0.77 mag) than the kcorrect outputs, because the Hubble constant is smaller, and thus things are further away.

How can I project onto filter XXX?

; First enumerate the filters you want to project onto:
fs = ['galex_FUV.par','bessell_U.par','bessell_B.par']

; Then project the SEDs into the variable maggies
k_projection_table, maggies, vm # coeffs, lambda, redshifts, fs, zmin=0,zmax=0,nz=1

lambda, vm and coeffs come from the routine kcorrect.

redshifts & fs are from you. zmin,zmax and nz are set so that you will be given the maggies at the redshifts you specify.